Leetcode 62: Unique Paths, Combinatorics, & Catalan Numbers
Coming Soon

Leetcode: 62 - Unique Paths

Problem Statement:

• Given the two integers m and n, return the number of possible unique paths you can take to reach the bottom-right corner.
• You can only move either down or right at any point in time.
• Link: https://leetcode.com/problems/unique-paths/

Algorithmic Solution:

Dynamic Programming

        // generate unique paths
          
        const rows = m;
        const columns = n;
        var row_index = 0;
        var col_index = 0;
      
      
        var grid_arr = []; // holds row and column numbers [(0,0),(0,1), (0,2) (0,2)], [(1,0),(1,1), (1,2) (1,2)], etc.
        var path = []; // holds individual paths
        var path_box = []; // holds final list of paths
        
      
        function generate_paths(grid_arr, path, row_index, col_index) {

          // If bottom-right cell reached, add path to path_box
          if (row_index === rows - 1 && col_index === columns - 1) {
            path.push(grid_arr[row_index][col_index]);
            path_box.push(path.slice());
            path.pop();
            return;
          }
        
          // Check boundary cases. Check if we are outside of the grid
          if (row_index < 0 || row_index >= rows || col_index < 0 || col_index >= columns) {
            return;
          }
        

          // Include current cell in path
          path.push(grid_arr[row_index][col_index]);
      
          // Move right in the matrix
          if (col_index + 1 < columns) {
            generate_paths(grid_arr, path, row_index, col_index + 1);
          }
        
          // Move down in the matrix
         if (row_index + 1 < rows) {
            generate_paths(grid_arr, path, row_index + 1, col_index);
          }
         
          // Backtrack. Remove the current cell from the current path
          path.pop();
        }
      
       generate_paths(grid_arr, path, row_index, col_index); 
      

Combinatorics Solution:

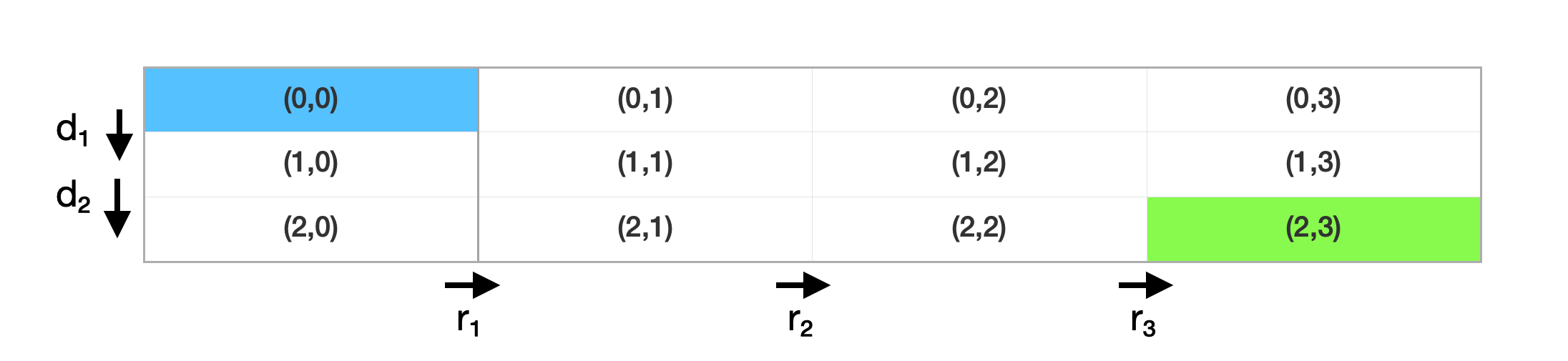
For the sake of example, take m == 3 (rows) and n == 4 (columns). We get a 3x4 grid as seen below.
To get from the start node to the end node we have two options: move right or move down. An important point of note for this problem is that our grid takes on a "taxicab" or "manhattan" geometry.

• From wikipedia: "The latter names refer to the rectilinear street layout on the island of Manhattan, where the shortest path a taxi travels between two points is the sum of the absolute values of distances that it travels on avenues and on streets."
• In \(\mathbb{R}^2\), the taxicab distance between \(p = (p_1,p_2)\) and \(q = (q_1,q_2)\) is \(\left\lvert p_1-q_2 \right\rvert + \left\lvert p_2 - q_2 \right\rvert \).
• https://en.wikipedia.org/wiki/Taxicab_geometry

Below are a number of possible paths when we move either down \((d_1,d_2)\) or right \((r_1,r_2,r_3)\). Notice there are 5 moves in total for this example, or \((m-1) +(n-1)\) moves in general, to get from start to finish.

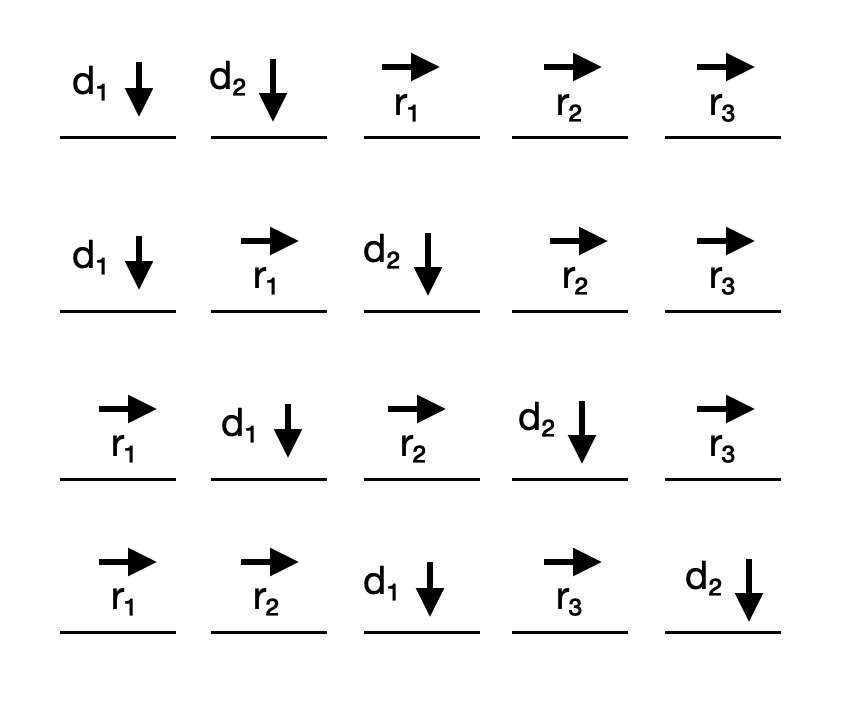
The first question now is: How many possible paths of length \((m-1) +(n-1)\) are there?

This is the same as asking how many, in our example, 5-long permutations there are. The solution is 5 factorial (5!) which evaluates to 120.

While our solution does account for all possible permutations, it fails to account for redundancies in direction choices. This is to say that \((d_1 == d_2)\) and \((r_1 == r_2 == r_3)\). I.e. if you flip \(d_1\) and \(d_2\) in the first example path, you still get the same path wherein you are moving down twice, then right 3 times.

To account for this, we have to divide out the number of permutations, or ways we can order, the possible down moves. In this case, that means dividing by 2 factorial (2!). Dividing by 2! leaves us with paths without redundancies occurring due to the ordering of our down moves.

\((d_1,d_2,r_1,r_2,r_3)\) and \((d_2,d_1,r_1,r_2,r_3)\) are the same path when getting from start to finish so we only take the first path when counting the total number of paths.

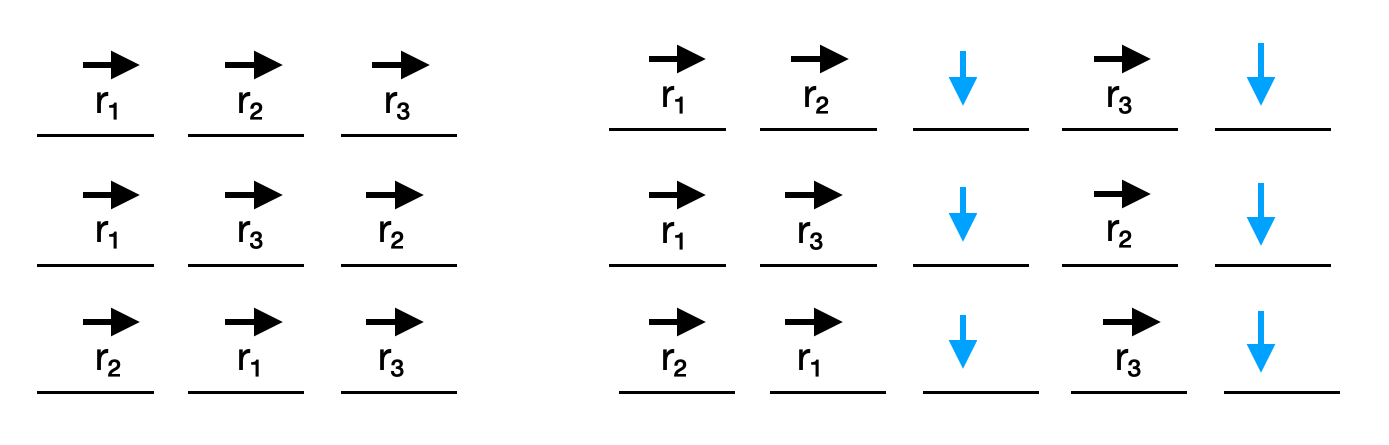
Similarly, we divide out by the number of right move permutations, in this case 3 factorial (3!). The bellow shows three orderings of right moves that could be divided out.
Notice the position of the down moves (blue) in the path, relative to any right moves, stays the same.

At the end, we are left with the following formula and solution:

\(\frac{ ((m-1) + (n-1))!}{(m-1)! \space (n-1)!}\)